エクセルのグラフ機能を使って素数の不思議を垣間見ます。
1000個の素数リストを作ります。
| 番号 n | 素数値 S | S/n(Sをnで割る) | 差分(前の素数との差) |
| 1 | 2 | 2.000 | 1(とりあえず1とした) |
| 2 | 3 | 1.500 | 1 |
| 3 | 5 | 1.667 | 2 |
| 4 | 7 | 1.750 | 2 |
| 5 | 11 | 2.200 | 4 |
| 6 | 13 | 2.167 | 2 |
という表をnが1~1229(1000個超えました)を作る。
この表の値でグラフを作成してみます。横軸はnです。
まず、S-n図。単純に番号と素数をグラフ化しただけです。
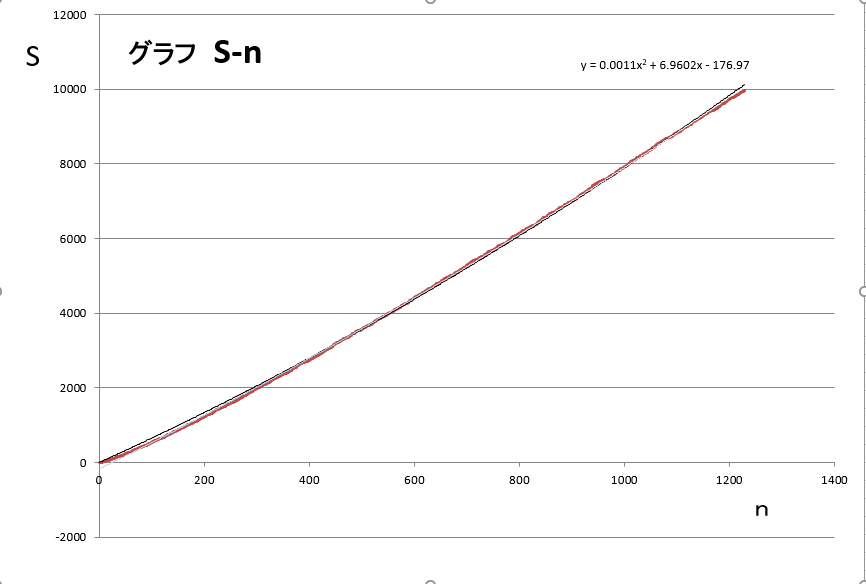
近似関数も表示してみました。多少ズレてますが、なんか法則がありそうです。近似関数の表示もONにしてあります。
次は、S/n-nのグラフ。
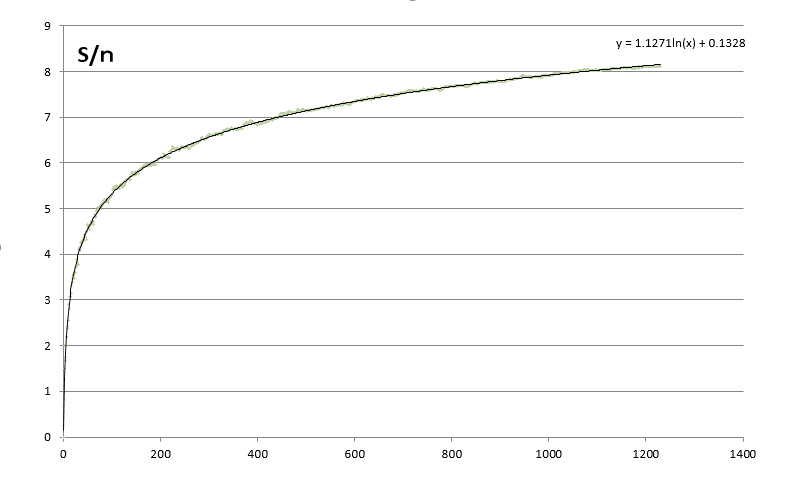
近似というか相関でしょうか。でも、こんな感じでまとまるのも面白いです。
差分は散布図にしてみました。n番目(横軸)の差分(縦軸)です。
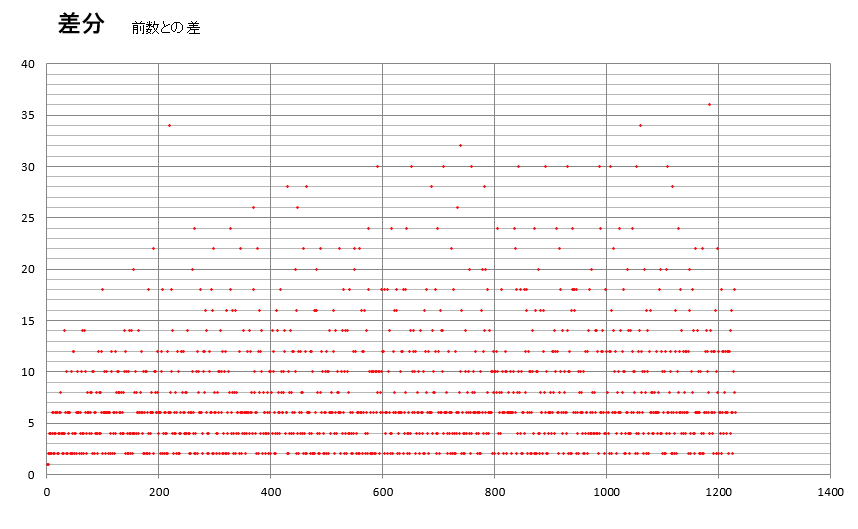
当たり前ですが、差分は偶数です。最初の1は2と3の差分なので1です。差分は2,4,6が多いです。200を超えたあたりにぽつんと差分34の点があります。217番1327の次の218番1361の差です。
なんとなく対数グラフのような相関が見えますが、上の例外みたいな点もあるので、やはり素数は不思議です。